|
|

|
Аттракторы
| |
| Asya | Дата: Суббота, 01.10.2011, 16:50 | Сообщение # 1 |
 Знающий
Группа: Совет гильдии
Сообщений: 837
Статус: Вне сайта
| 


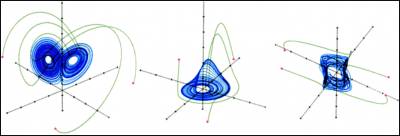
Аттракторы — это геометрические структуры, характеризующие поведение в фазовом пространстве по прошествии длительного времени. Грубо говоря, аттрактор — это то, к чему система стремится прийти, к чему она притягивается. Здесь аттракторы показаны синим цветом, а начальные состояния — красным. Траектории, выйдя из начальных состояний, в конце концов приближаются к аттракторам. Самый простой тип аттрактора — неподвижная точка (вверху слева). Такой аттрактор соответствует поведению маятника при наличии трения; маятник всегда приходит в одно и то же положение покоя независимо от того, как он начал колебаться (см. правую половину рис. 2). Следующий, более сложный аттрактор — предельный цикл (вверху в центре), который имеет форму замкнутой петли в фазовом пространстве. Предельный цикл описывает устойчивые колебания, такие, как движение маятника в часах или биение сердца. Сложному колебанию, или квазипериодическому движению, соответствует аттрактор в форме тора (вверху справа). Все три аттрактора предсказуемы: их поведение можно прогнозировать с любой точностью. Хаотические аттракторы соответствуют непредсказуемому движению и имеют более сложную геометрическую форму. Три примера хаотических аттракторов изображены в нижнем ряду; они получены (слева направо) Э. Лоренцем, О. Рёсслером и одним из авторов (Шоу) соответственно путём решения простых систем дифференциальных уравнений с трёхмерным фазовым пространством.
Ангел яростнее любого Дракона, но только не в битве, а в попытках достучаться до нас, и напомнить, кто мы есть на самом деле, ибо только мы сами имеем полную власть над миром, который создаем вокруг себя – то, что ты сейчас воображаешь, тот мир, который выстраиваешь в голове, может быть реальнее всякой боли…
|
| |
|
|
| Asya | Дата: Суббота, 01.10.2011, 16:51 | Сообщение # 2 |
 Знающий
Группа: Совет гильдии
Сообщений: 837
Статус: Вне сайта
| 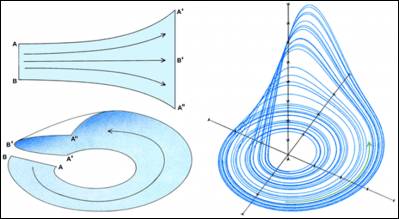
Хаотический аттрактор имеет гораздо более сложное строение, чем предсказуемые аттракторы — точка, предельный цикл или тор. В крупном масштабе хаотический аттрактор есть неровная поверхность со складками. Показаны этапы образования хаотического аттрактора на примере аттрактора Рёсслера (справа). Сначала близкие траектории на объекте расходятся экспоненциально (вверху слева); расстояние между соседними траекториями увеличивается примерно вдвое. Чтобы остаться в конечной области, объект складывается (внизу слева): поверхность сгибается и её края соединяются. Аттрактор Рёсслера наблюдался во многих системах, от потоков жидкости до химических реакций; этот факт иллюстрирует максиму Эйнштейна о том, что природа предпочитает простые структуры.
Ангел яростнее любого Дракона, но только не в битве, а в попытках достучаться до нас, и напомнить, кто мы есть на самом деле, ибо только мы сами имеем полную власть над миром, который создаем вокруг себя – то, что ты сейчас воображаешь, тот мир, который выстраиваешь в голове, может быть реальнее всякой боли…
|
| |
|
|
| Asya | Дата: Суббота, 01.10.2011, 16:59 | Сообщение # 3 |
 Знающий
Группа: Совет гильдии
Сообщений: 837
Статус: Вне сайта
| Экспериментальные данные подтверждают гипотезу о том, что в основе некоторых типов случайных движений в жидкости лежат хаотические аттракторы. Здесь приведены сделанные друг за другом фотографии поверхности воды в ячейке Куэтта, состоящей из двух вложенных цилиндров. Пространство между цилиндрами заполнено водой, и внутренний цилиндр вращается с определённой угловой скоростью (a). По мере увеличения скорости течение жидкости становится всё сложнее (b), превращается в нерегулярное ©, а затем хаотическое (d).

(а)

(b)

©

(d)
Ангел яростнее любого Дракона, но только не в битве, а в попытках достучаться до нас, и напомнить, кто мы есть на самом деле, ибо только мы сами имеем полную власть над миром, который создаем вокруг себя – то, что ты сейчас воображаешь, тот мир, который выстраиваешь в голове, может быть реальнее всякой боли…
|
| |
|
|
|
|


